Originally published on Brooking Institution's Brown Center Chalkboard, July 3, 2013
The latest charter school study from the Center for Research on Education
Outcomes (CREDO) was released last week. It provided an update to a similar report published in 2009. The 2009 study had found that charter schools underperformed traditional public schools (TPS) by about .01 standard deviations on state achievement tests of reading and .03 standard deviations in math. The new study showed charters doing better, out-performing TPS by .01 standard deviations in reading and scoring about the same as TPS in math.
How did the press react? The NY Times described charter school performance as “improving.” Associated Press concluded “charter school students are faring better than they were four years ago, surpassing those in public schools in reading gains and keeping pace in math.” The Washington Post reported that charters “are growing more effective but most don’t produce better academic results when compared to traditional public schools.”
All of these statements are accurate. What I discuss in this Chalkboard post is whether the sector differences uncovered by either of the CREDO studies are significant. Not statistically significant--that's an indication of whether differences are larger than the amount attributable to statistical noise. Statistical significance is a result of two factors: 1) sample size and 2) size or magnitude of an effect. The CREDO sample size is enormous, about 1.5 million charter students along with a matched group of TPS students. A problem with huge samples is that they often detect statistically significant effects that aren’t very large or important.
That’s the question explored here. Are the differences reported by CREDO large enough to be significant in the real world? Critics of charter schools repeatedly cite the 2009 results as evidence that charters have failed. Charter advocates are no doubt champing at the bit to cite the 2013 results in rebuttal. These competing interpretations obscure the CREDO studies’ main finding: achievement differences between charters and TPS are extremely small, so tiny, in fact, that they lack real world significance. The main differences between sectors—that is, between charters and TPS–range between .01 and .03 standard deviations, depending on whether the results are from 2009 or 2013, indicating achievement gains in reading or math, confined to one year’s or three years’ growth, based on the original 16 states in the 2009 study or the 27 states of the 2013 study, and so on.
Let’s see what .01 and .03 differences look like in other settings.
Interpreting SD Differences
Standard deviation (SD) is a measure of variation. Statistical studies often express differences between treatment and control groups in SD units, known as effect sizes. An influential paper by Jacob Cohen in 1969 proposed categorizing effect sizes as small (at least 0.2) , medium (at least 0.5), or large (at least 0.8). Cohen reasoned that a 0.2 difference is usually too small to be detectable to the naked eye. He gave as an example the difference in height of typical 15 and 16 year old American girls. It is impossible to discern a difference. A medium effect, 0.5 SD, which is the difference between 14 year old and 18 year old females, is surely large enough to be detectable by sight. And a large effect, 0.8 SD, corresponds to the difference between 13 and 18 year old females—difficult to miss.
Let’s stick to height comparisons and consider the CREDO effects. The 0.01 and 0.03 differences are far below Cohen’s 0.2 threshold for qualifying as even small effects. American men average 5’ 10” in height with a SD of 3.0”. That means 0.01 SD is equal to about 0.03 inches and 0.03 SD is equal to about .09 inches. That’s not noticeable. Think of it this way. A ream of paper is approximately 2.25 inches thick. There are 500 sheets to a ream. You attend a public talk given by a close friend, a guy who is about 5’ 10” tall. He stands behind a podium on 7 sheets of paper. That’s a bit larger than a 0.01 SD addition to his height. Would you go up to him afterwards and say, “Wow, you look taller today.” I doubt it. What if he stood on 20 sheets of paper (about 0.03 SDs)? Nope. You wouldn’t notice a difference.
Here’s an illustration from the world of finance. The Dow Jones Industrial Average (DJIA) is followed broadly as an index of stock market performance. Stocks have experienced a lot of volatility over the past five years, taking investors on a roller coaster ride, first sharply down and then up. I downloaded the daily closing figures for the DJIA from July 1, 2008 to July 1, 2013 from the website of the St. Louis Federal Reserve Bank. The standard deviation of daily change for the DJIA during this time frame was 107 points. That means a 0.01 SD change is approximately a single point on the Dow; a 0.03 change is 3.21 Dow points. Would you be concerned about your 401K if the market fell 3.21 Dow points tomorrow? Would you be excited if it went up that amount? I hope not.
Let’s turn to an education statistic. Most people who follow education are aware of the National Assessment of Educational Progress (NAEP), but only the statistically inclined pay much attention to the standard deviations of NAEP tests. The national average on the 2011 NAEP eighth grade reading test was 265 with a SD of 34. That means a gain of 0.01 SD is about one-third of a single point (0.34) on the NAEP scale. A gain of 0.03 SD is approximately one point. I don’t know a single analyst who gets excited over a one point change in NAEP scores. The national NAEP score for 4th grade math, on the other hand, increased by 28 points from 1990 to 2011. That’s the equivalent of 0.875 SD (using the 1990 SD of 32)–or more than 87 times larger than the charter-traditional public schools (TPS) difference, surely a substantive change, and a “large” difference according to Cohen’s criteria.
How Other Metrics Can Make a Small Effect Appear Large
If the CREDO effects are so small, why do some people react to them as if they are large? The CREDO team uses other metrics to express charter-TPS differences, and I believe one of them in particular—horse racing the sectors by reporting the percentage of charters scoring higher, the same as, or lower than TPS—can mislead people into thinking small effects are large. My comments here are not meant as criticism of the CREDO studies. They have made a valuable contribution to our knowledge of charter schools. Researchers often try to express their statistical findings in a manner that lay readers can grasp. But there are dangers in doing that.
I have tabled the percentages CREDO reported for mathematics in the 2009 and 2013 reports.
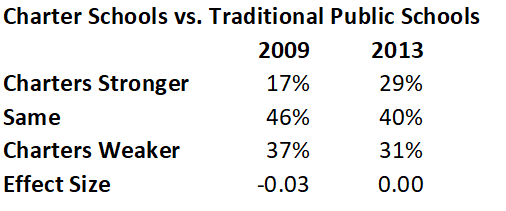
In 2009, 17% of charter schools outscored traditional public schools in math, 46% scored about the same, and 37% were weaker. In 2013, 29% of charters outscored TPS, 40% scored about the same, and 31% were weaker. You can see that this presentation magnifies the tiny student-level differences (shown in SD units, as effect sizes, in the bottom row). The CREDO study calculated charter-TPS differences by matching charter students–based on observed characteristics such as race, gender, and previous test score–with a similar student in the traditional public schools from which the charters draw students. Schools were not matched so these estimates are extrapolations from the student-level data.
Critics of charter schools summarized the 2009 findings as showing, “Only 17% of charters were higher-performing than traditional public schools. The other 83% were either no different or lower performing.” That’s accurate. It also sounds pretty damning for charter schools.
An important question to ask is: what is the expected distribution? An illustration with coins will underscore the relevance of the question. Two coins are labeled “A” and “B.” They represent charter and traditional public schools. Let’s consider heads to be high performance and tails to be low performance. We know apriori two important facts about the coins: 1) They are identical to each other, 2) Each has an equal chance of producing high performance (that is, of getting a heads).
Flipping the coins an infinite number of times produces the following frequency of outcomes.
Coin A vs. Coin B, infinite number of flips (Heads is stronger, Tails is weaker)
|
Conclusion |
Outcome of flip |
Frequency |
|
Coin A is stronger |
H-T |
25% |
|
Same |
H-H or T-T |
50% |
|
Coin B is stronger |
T-H |
25% |
Now consider the following statement: “Coin A is disappointing. It only outperformed Coin B 25% of the time and performed the same or worse 75% of the time.” The statement is true, but it obscures the fact that the performance of the two coins is identical. Nothing surprising has occurred. And the exact same disappointment can be expressed about Coin B’s performance.
Back to the CREDO percentages and the question regarding expected frequencies. I already know from CREDO’s student level data that the two sectors’ scores are approximately equal. The charter-TPS comparison is not precisely analogous to the coin example (for example, the distributions will be different because coin flips are binary, test scores are continuous); nevertheless, I would expect that one sector would outperform the other somewhere in the ballpark of 25% of the time and perform the same or worse 75% of the time. The actual “same or worse” figure for charters was 83% in 2009. In 2013, it was 71%.
Conclusion
Here I have provided real world examples that illustrate the negligible charter-TPS sector differences uncovered by the 2009 and 2013 CREDO studies. The two sectors perform about the same. Claims that the CREDO studies demonstrate the success or failure of one sector or the other are based on analyses that make small differences appear much larger than they really are.