Originally published on Brooking Institution's Brown Center Chalkboard, July 9, 2015
This is part two of my analysis of instruction and Common Core’s implementation. I dubbed the three-part examination of instruction “The Good, The Bad, and the Ugly.” Having discussed “the “good” in part one, I now turn to “the bad.” One particular aspect of the Common Core math standards—the treatment of standard algorithms in whole number arithmetic—will lead some teachers to waste instructional time.
A Model of Time and Learning
In 1963, psychologist John B. Carroll published a short essay, “A Model of School Learning” in Teachers College Record. Carroll proposed a parsimonious model of learning that expressed the degree of learning (or what today is commonly called achievement) as a function of the ratio of time spent on learning to the time needed to learn.
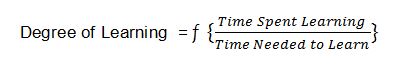
The numerator, time spent learning, has also been given the term opportunity to learn. The denominator, time needed to learn, is synonymous with student aptitude. By expressing aptitude as time needed to learn, Carroll refreshingly broke through his era’s debate about the origins of intelligence (nature vs. nurture) and the vocabulary that labels students as having more or less intelligence. He also spoke directly to a primary challenge of teaching: how to effectively produce learning in classrooms populated by students needing vastly different amounts of time to learn the exact same content.[i]
The source of that variation is largely irrelevant to the constraints placed on instructional decisions. Teachers obviously have limited control over the denominator of the ratio (they must take kids as they are) and less than one might think over the numerator. Teachers allot time to instruction only after educational authorities have decided the number of hours in the school day, the number of days in the school year, the number of minutes in class periods in middle and high schools, and the amount of time set aside for lunch, recess, passing periods, various pull-out programs, pep rallies, and the like. There are also announcements over the PA system, stray dogs that may wander into the classroom, and other unscheduled encroachments on instructional time.
The model has had a profound influence on educational thought. As of July 5, 2015, Google Scholar reported 2,931 citations of Carroll’s article. Benjamin Bloom’s “mastery learning” was deeply influenced by Carroll. It is predicated on the idea that optimal learning occurs when time spent on learning—rather than content—is allowed to vary, providing to each student the individual amount of time he or she needs to learn a common curriculum. This is often referred to as “students working at their own pace,” and progress is measured by mastery of content rather than seat time. David C. Berliner’s 1990 discussion of time includes an analysis of mediating variables in the numerator of Carroll’s model, including the amount of time students are willing to spend on learning. Carroll called this persistence, and Berliner links the construct to student engagement and time on task—topics of keen interest to researchers today. Berliner notes that although both are typically described in terms of motivation, they can be measured empirically in increments of time.
Most applications of Carroll’s model have been interested in what happens when insufficient time is provided for learning—in other words, when the numerator of the ratio is significantly less than the denominator. When that happens, students don’t have an adequate opportunity to learn. They need more time.
As applied to Common Core and instruction, one should also be aware of problems that arise from the inefficient distribution of time. Time is a limited resource that teachers deploy in the production of learning. Below I discuss instances when the CCSS-M may lead to the numerator in Carroll’s model being significantly larger than the denominator—when teachers spend more time teaching a concept or skill than is necessary. Because time is limited and fixed, wasted time on one topic will shorten the amount of time available to teach other topics. Excessive instructional time may also negatively affect student engagement. Students who have fully learned content that continues to be taught may become bored; they must endure instruction that they do not need.
Standard Algorithms and Alternative Strategies
Jason Zimba, one of the lead authors of the Common Core Math standards, and Barry Garelick, a critic of the standards, had a recent, interesting exchange about when standard algorithms are called for in the CCSS-M. A standard algorithm is a series of steps designed to compute accurately and quickly. In the U.S., students are typically taught the standard algorithms of addition, subtraction, multiplication, and division with whole numbers. Most readers of this post will recognize the standard algorithm for addition. It involves lining up two or more multi-digit numbers according to place-value, with one number written over the other, and adding the columns from right to left with “carrying” (or regrouping) as needed.
The standard algorithm is the only algorithm required for students to learn, although others are mentioned beginning with the first grade standards. Curiously, though, CCSS-M doesn’t require students to know the standard algorithms for addition and subtraction until fourth grade. This opens the door for a lot of wasted time. Garelick questioned the wisdom of teaching several alternative strategies for addition. He asked whether, under the Common Core, only the standard algorithm could be taught—or at least, could it be taught first. As he explains:
Delaying teaching of the standard algorithm until fourth grade and relying on place value “strategies” and drawings to add numbers is thought to provide students with the conceptual understanding of adding and subtracting multi-digit numbers. What happens, instead, is that the means to help learn, explain or memorize the procedure become a procedure unto itself and students are required to use inefficient cumbersome methods for two years. This is done in the belief that the alternative approaches confer understanding, so are superior to the standard algorithm. To teach the standard algorithm first would in reformers’ minds be rote learning. Reformers believe that by having students using strategies in lieu of the standard algorithm, students are still learning “skills” (albeit inefficient and confusing ones), and these skills support understanding of the standard algorithm. Students are left with a panoply of methods (praised as a good thing because students should have more than one way to solve problems), that confuse more than enlighten.
Zimba responded that the standard algorithm could, indeed, be the only method taught because it meets a crucial test: reinforcing knowledge of place value and the properties of operations. He goes on to say that other algorithms also may be taught that are consistent with the standards, but that the decision to do so is left in the hands of local educators and curriculum designers:
In short, the Common Core requires the standard algorithm; additional algorithms aren’t named, and they aren’t required…Standards can’t settle every disagreement—nor should they. As this discussion of just a single slice of the math curriculum illustrates, teachers and curriculum authors following the standards still may, and still must, make an enormous range of decisions.
Zimba defends delaying mastery of the standard algorithm until fourth grade, referring to it as a “culminating” standard that he would, if he were teaching, introduce in earlier grades. Zimba illustrates the curricular progression he would employ in a table, showing that he would introduce the standard algorithm for addition late in first grade (with two-digit addends) and then extend the complexity of its use and provide practice towards fluency until reaching the culminating standard in fourth grade. Zimba would introduce the subtraction algorithm in second grade and similarly ramp up its complexity until fourth grade.
It is important to note that in CCSS-M the word “algorithm” appears for the first time (in plural form) in the third grade standards:
3.NBT.2 Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
The term “strategies and algorithms” is curious. Zimba explains, “It is true that the word ‘algorithms’ here is plural, but that could be read as simply leaving more choice in the hands of the teacher about which algorithm(s) to teach—not as a requirement for each student to learn two or more general algorithms for each operation!”
I have described before the “dog whistles” embedded in the Common Core, signals to educational progressives—in this case, math reformers—that despite these being standards, the CCSS-M will allow them great latitude. Using the plural “algorithms” in this third grade standard and not specifying the standard algorithm until fourth grade is a perfect example of such a dog whistle.
Why All the Fuss about Standard Algorithms?
It appears that the Common Core authors wanted to reach a political compromise on standard algorithms.
Standard algorithms were a key point of contention in the “Math Wars” of the 1990s. The 1997 California Framework for Mathematics required that students know the standard algorithms for all four operations—addition, subtraction, multiplication, and division—by the end of fourth grade.[ii] The 2000 Massachusetts Mathematics Curriculum Framework called for learning the standard algorithms for addition and subtraction by the end of second grade and for multiplication and division by the end of fourth grade. These two frameworks were heavily influenced by mathematicians (from Stanford in California and Harvard in Massachusetts) and quickly became favorites of math traditionalists. In both states’ frameworks, the standard algorithm requirements were in direct opposition to the reform-oriented frameworks that preceded them—in which standard algorithms were barely mentioned and alternative algorithms or “strategies” were encouraged.
Now that the CCSS-M has replaced these two frameworks, the requirement for knowing the standard algorithms in California and Massachusetts slips from third or fourth grade all the way to sixth grade. That’s what reformers get in the compromise. They are given a green light to continue teaching alternative algorithms, as long as the algorithms are consistent with teaching place value and properties of arithmetic. But the standard algorithm is the only one students are required to learn. And that exclusivity is intended to please the traditionalists.
I agree with Garelick that the compromise leads to problems. In a 2013 Chalkboard post, I described a first grade math program in which parents were explicitly requested not to teach the standard algorithm for addition when helping their children at home. The students were being taught how to represent addition with drawings that clustered objects into groups of ten. The exercises were both time consuming and tedious. When the parents met with the school principal to discuss the matter, the principal told them that the math program was following the Common Core by promoting deeper learning. The parents withdrew their child from the school and enrolled him in private school.
The value of standard algorithms is that they are efficient and packed with mathematics. Once students have mastered single-digit operations and the meaning of place value, the standard algorithms reveal to students that they can take procedures that they already know work well with one- and two-digit numbers, and by applying them over and over again, solve problems with large numbers. Traditionalists and reformers have different goals. Reformers believe exposure to several algorithms encourages flexible thinking and the ability to draw on multiple strategies for solving problems. Traditionalists believe that a bigger problem than students learning too few algorithms is that too few students learn even one algorithm.
I have been a critic of the math reform movement since I taught in the 1980s. But some of their complaints have merit. All too often, instruction on standard algorithms has left out meaning. As Karen C. Fuson and Sybilla Beckmann point out, “an unfortunate dichotomy” emerged in math instruction: teachers taught “strategies” that implied understanding and “algorithms” that implied procedural steps that were to be memorized. Michael Battista’s research has provided many instances of students clinging to algorithms without understanding. He gives an example of a student who has not quite mastered the standard algorithm for addition and makes numerous errors on a worksheet. On one item, for example, the student forgets to carry and calculates that 19 + 6 = 15. In a post-worksheet interview, the student counts 6 units from 19 and arrives at 25. Despite the obvious discrepancy—(25 is not 15, the student agrees)—he declares that his answers on the worksheet must be correct because the algorithm he used “always works.”[iii]
Math reformers rightfully argue that blind faith in procedure has no place in a thinking mathematical classroom. Who can disagree with that? Students should be able to evaluate the validity of answers, regardless of the procedures used, and propose alternative solutions. Standard algorithms are tools to help them do that, but students must be able to apply them, not in a robotic way, but with understanding.
Conclusion
Let’s return to Carroll’s model of time and learning. I conclude by making two points—one about curriculum and instruction, the other about implementation.
In the study of numbers, a coherent K-12 math curriculum, similar to that of the previous California and Massachusetts frameworks, can be sketched in a few short sentences. Addition with whole numbers (including the standard algorithm) is taught in first grade, subtraction in second grade, multiplication in third grade, and division in fourth grade. Thus, the study of whole number arithmetic is completed by the end of fourth grade. Grades five through seven focus on rational numbers (fractions, decimals, percentages), and grades eight through twelve study advanced mathematics. Proficiency is sought along three dimensions: 1) fluency with calculations, 2) conceptual understanding, 3) ability to solve problems.
Placing the CCSS-M standard for knowing the standard algorithms of addition and subtraction in fourth grade delays this progression by two years. Placing the standard for the division algorithm in sixth grade continues the two-year delay. For many fourth graders, time spent working on addition and subtraction will be wasted time. They already have a firm understanding of addition and subtraction. The same thing for many sixth graders—time devoted to the division algorithm will be wasted time that should be devoted to the study of rational numbers. The numerator in Carroll’s instructional time model will be greater than the denominator, indicating the inefficient allocation of time to instruction.
As Jason Zimba points out, not everyone agrees on when the standard algorithms should be taught, the alternative algorithms that should be taught, the manner in which any algorithm should be taught, or the amount of instructional time that should be spent on computational procedures. Such decisions are made by local educators. Variation in these decisions will introduce variation in the implementation of the math standards. It is true that standards, any standards, cannot control implementation, especially the twists and turns in how they are interpreted by educators and brought to life in classroom instruction. But in this case, the standards themselves are responsible for the myriad approaches, many unproductive, that we are sure to see as schools teach various algorithms under the Common Core.
[i] Tracking, ability grouping, differentiated learning, programmed learning, individualized instruction, and personalized learning (including today’s flipped classrooms) are all attempts to solve the challenge of student heterogeneity.
[ii] An earlier version of this post incorrectly stated that the California framework required that students know the standard algorithms for all four operations by the end of third grade. I regret the error.
[iii] Michael T. Battista (2001). “Research and Reform in Mathematics Education,” pp. 32-84 in The Great Curriculum Debate: How Should We Teach Reading and Math? (T. Loveless, ed., Brookings Instiution Press).